Ytelsesmål for maskinlæringsmodeller (KI-faktaark 3)

Om faktaarket

Formålet med faktaarket er å gi en kort innføring i ytelsesmål for noen hovedtyper av maskinlæringsmodeller.

Ytelsesmål for maskinlæringsmodeller

Faktaarket beskriver ytelsesmål for følgende hovedtyper maskinlæringsmodeller:

• Binære klassifikasjonsmodeller
• Klassifikasjon med flere klasser
• Regresjonsmodeller
• Segmentering og objektdeteksjon i bilder
• Generative modeller

Binære klassifikasjonsmodeller

Den enkleste modellkategorien å evaluere er binære klassifikasjonsmodeller, hvor modellen velger mellom to kategorier, som "syk" eller "frisk".

Sensitivitet og spesifisitet

Sensitivitet og spesifisitet brukes for å kvantifisere ytelse av en modell eller en test. Under er dette eksemplifisert ved en diagnostisk test for en sykdom:

• Sensitivitet er modellens evne til å korrekt identifisere de med sykdommen (sanne positive) blant de som faktisk er syke. Med andre ord, det er sannsynligheten for at en syk person vil ha en positiv test.
• Spesifisitet er modellens evne til å korrekt identifisere de uten sykdommen (sanne negative) blant de som faktisk er friske. Med andre ord, det er sannsynligheten for at en frisk person vil ha en negativ test.

Positiv og negativ prediktiv verdi

Positiv prediktiv verdi (PPV) er sannsynligheten for at en person som fikk positivt testresultat virkelig er syk. Tilsvarende for negativ prediktiv verdi (NPV). Disse måler altså hvor ofte modellen har rett når den kommer med en positiv eller negativ prediksjon.

Disse prediktive verdiene påvirkes sterkt av sykdommens forekomst (prevalens) i utvalget som testes. En test med høy sensitivitet kan ha lav positiv prediktiv verdi hvis den gjøres hos grupper med lav sykdomsprevalens.1 Hvis man skal tallfeste ytelsen til en maskinlæringsmodell i seg selv, er det derfor bedre å bruke sensitivitet og spesifisitet fordi PPV og NPV er avhengig av prevalensen i befolkningen. I rabies-eksempelet er det for eksempel ikke rimelig å si at modellen er dårlig selv om PPV er nær 0. Hvis man skal bruke en maskinlæringsmodell i en klinisk situasjon for å ta beslutninger om f.eks. behandling, er derimot de prediktive verdiene sentrale, og sensitivitet og spesifisitet mindre relevant.

Krysstabell

Ytelsen til en klassifikasjonsmodell på et gitt datasett oppsummeres ofte med en matrise, også kalt krysstabell, se Figur 1. Krysstabellen viser antall faktiske tilfeller i kolonnene og antall predikerte tilfeller i radene. Relevante målinger kan deretter beregnes ut fra oppføring i tabellen. Krysstabeller er en nyttig måte å beskrive modellytelse på fordi de er intuitive å lese, og dekker alle mulige kombinasjoner av korrekte og feilaktige prediksjoner.

ROC-kurve og AUC

For binære klassifikasjonsmodeller vil det normalt ligge en kontinuerlig modell under, som tilordner en risikoskår til hvert inndata, og da vil en ROC-kurve (engelsk: Receiver Operating Characteristics curve) fange opp den relevante informasjonen². Punktene på denne kurven korresponderer med forskjellige terskelverdier for den underliggende risikoskåren. X-aksen er andelen falske positive (1 – spesifisitet) mens y-aksen er andel sanne positive (sensitivitet). Kurven representerer avveiningen mellom sensitivitet og spesifisitet, og hvis man f.eks. krever et bestemt nivå for sensitivitet (som 90%), kan man lese av hva den tilhørende spesifisiteten blir.

Arealet under ROC-kurven (AUC) er et vanlig generelt ytelsesmål, som kan benyttes hvis man ikke har noen klare føringer på sensitivitet eller spesifisitet. AUC er et tall mellom 0 og 1. En modell med 100% gale prediksjoner har en AUC på 0, mens en modell som har 100% riktige prediksjoner har en AUC på 1.  Det er derfor et mål på hvor godt risikoskåren skiller mellom positive og negative tilfeller. AUC har en ekvivalent tolkning som sannsynligheten for at et tilfeldig positivt tilfelle får høyere risikoskår enn en tilfeldig negativ. Hvis man ikke har mulighet til å justere noen terskelverdi, vil sensitivitet og spesifisitet være faste verdier, som kan plottes som et punkt i det samme diagrammet.   

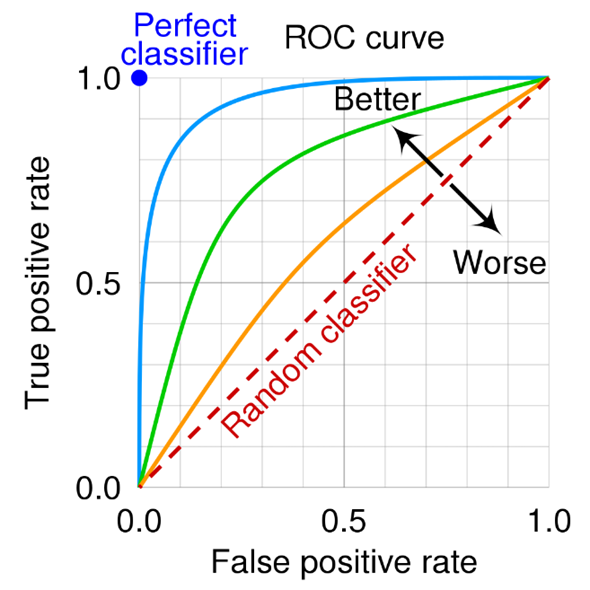
ROC-kurven og AUC-målet er i prinsippet uavhengige av balansen i datamaterialet, og påvirkes for eksempel ikke hvis man dobler antallet negative tilfeller, men dette forutsetter at de man legger til trekkes fra samme underliggende fordeling som dem man har i utgangspunktet. AUC kan brukes til overordnet sammenlikning av maskinlæringsmodeller.

Klassifikasjonsmodeller gir ofte en sannsynlighet mellom 0 og 1 for at et tilfelle er positivt, i stedet for et binært resultat. Dette betyr at modellen gir en verdi som indikerer hvor sannsynlig det er at et tilfelle er positivt. For å klassifisere tilfellet som positivt eller negativt, setter man en terskel for sannsynligheten.  Hvis verdien overstiger terskelen, klassifiserer modellen tilfellet som positivt; hvis verdien ikke overstiger terskelen, blir tilfellet klassifisert som negativt.

Terskelverdier

Før man gjør en anskaffelse bør man ta stilling til hvordan maskinlæringsmodellen skal brukes i praksis og foreta et valg om terskelverdi, og dermed prioritere mellom sensitivitet og spesifisitet. Denne avveiningen avhenger av å veie opp helsekonsekvensene ved å gå glipp av en diagnose med de eventuelle helseøkonomiske og andre implikasjoner overdiagnostisering medfører.

Et eksempel er en maskinlæringsmodell som skal brukes i tidlige brystkreftscreeningstester. Evnen til å fange opp positive tilfeller kan være spesielt viktig. For eksempel bør ikke noen som faktisk har en ondartet svulst overses. Dette innebærer at modellen krever høy sensitivitet - dvs. andelen faktiske positive tilfeller som blir korrekt identifisert. Samtidig, hvis sensitivitet prioriteres overdrevent, blir modellens spesifisitet - dvs. andelen faktiske negative tilfeller som blir korrekt identifisert - uakseptabelt lav. I praksis betyr dette at modellen kan utløse for mange unødvendige konsultasjoner og prøver av personer som ikke har brystkreft.

Hvis derimot maskinlæringsmodellen skal brukes til testing på et senere punkt i utredningen, kan evnen til å korrekt oppdage negative tilfeller bli viktigere, altså et høyere nivå av spesifisitet. For mange falske positive prøvesvar kan gi feilaktig diagnostisering, som kan gi unødig engstelse hos pasienten eller medføre overbehandling. Det å pålitelig fange opp positive tilfeller er fortsatt viktig, så avveiningen med sensitivitet må vurderes.

Klassifikasjon med flere klasser

Maskinlæringsmodeller kan også brukes i situasjoner hvor det finnes mer enn to klasser, for eksempel hvis modellen skal predikere forskjellige sykdommer. Flere av metodene fra binær klassifikasjon kan tilpasses denne situasjonen, og man kan for eksempel beregne sensitivitet, spesifisitet eller prediktive verdier for hver klasse. Det finnes også generiske mål som tar sikte på å vurdere hvor godt modellen fungerer alt i alt, som nøyaktighet (accuracy på engelsk) eller det mer komplekse målet F1-skår. Selv om disse kan være nyttige i en vitenskapelig prosess hvor man utvikler og sammenlikner modeller, er det viktig at disse ytelsesmålene vurderes tverrfaglig med analyse- og domenekompetanse for en anskaffelsesprosess.

Krysstabeller er ekstra nyttig når man har flere klasser, siden den illustrerer hvilke klasser modellen har problemer med å skille fra hverandre. Figur 3 er en illustrasjon på en krysstabell for en modell som predikerer hvilken legegruppe i en ortopedisk klinikk som skal behandle en gitt henvisning, basert på henvisningsteksten.

Regresjonsmodeller

Mens klassifikasjonsmodeller predikerer valg mellom diskrete klasser, predikerer regresjonsmodeller kontinuerlige størrelser. For eksempel ville regresjonsmodeller være nødvendig for å forutsi hvor mange mennesker som vil oppsøke legevakten på en gitt dag, eller hvor mange sykehjemssenger som vil være nødvendig for pasienter som skrives ut fra sykehuset neste uke.

Ytelsesmål for regresjonsmodeller er basert på statistikk over avviket mellom faktisk og predikert verdi. Et vanlig mål er ‘Root mean square error’ (RMSE). Den beregnes ved at man kvadrerer avvikene (som gjør dem positive) og tar gjennomsnitt av disse. Så tar man kvadratroten av dette, som gir et resultat med samme enhet som verdien man forsøker å predikere. Et beslektet ytelsesmål er ‘Mean absolute error’ (MAE), som er gjennomsnittet av absoluttverdien av feilen. MAE kan virke lettere å tolke, men RMSE er ofte et mer relevant mål fordi den straffer store avvik og er knyttet til estimering av gjennomsnittsverdier. Hvis man for eksempel har to caser med like prediktorer og forskjellige utdata-verdier (10 og 20), må modellen lage et kompromiss. For å få lavest mulig RMSE (5), må modellen predikere gjennomsnittet (15), mens alle modeller som gir verdi mellom 10 og 20 vil få minimal MAE (også 5). Derfor er RMSE også mer brukt som kriterium under trening av modeller.

RMSE og MAE måler størrelsen på feilen modellen gjør, men uten å ta hensyn til hvor vanskelig oppgaven er. Hvis verdien man vil predikere varierer lite, vil selv en «modell» som alltid gjetter på gjennomsnittet ha lave verdier på RMSE og MAE. Målet R² tar hensyn til dette ved å estimere hvor mye mindre variansen til feilen er i forhold til variansen på verdien man predikerer. Jo, høyere R², jo mer av variasjonen har modellen forklart, og en perfekt modell har R² =1.

Feil med datainnsamling eller uvanlige hendelser kan resultere i “outliers”, som er ekstreme observasjoner. Håndtering av slike er noe av det vanskeligste i praktisk medisinsk statistikk. Hvis vi for eksempel modellerer liggetiden i sykehus og en pasient er registrert med en liggetid på 100 år, er det klart en feil, som må fjernes fra datamaterialet. Hvis modellen estimerer gjennomsnittlig liggetid med RMSE som mål, vil denne observasjonen dominere beregningene fullstendig. Men hva så, hvis en liggetid er 1, 2 eller 3 år? Hvis man setter en grense for hva som er mulige liggetider, har det mye å si akkurat hvor denne settes. En vanlig løsning er å bruke MAE i stedet, som matematisk betyr å predikere median i stedet for gjennomsnitt. Men dette løser ikke problemet hvis modellen skal brukes til å planlegge belegg på et sykehus, for hvis liggetider på 2 år er reelle, vil slike pasienter faktisk legge beslag på sengeressursen så lenge. Derfor må man ta stilling til hvilke datapunkter som er feilregistreringer og hvilke som er reelle ekstremverdier.

Segmentering og objektdeteksjon i bilder

KI-modeller som vurderer bilder, vil sjelden være begrenset til ren klassifisering eller regresjon, men vil normalt også markere hvilke deler av bildet som bidrar til konklusjonen. En segmenteringsoppgave kan for eksempel være å tegne inn nyrene i et MR-bilde. Fasiten vil bestå i en eksakt markering av nyrenes areal og målet er at modellen markerer de samme pikslene. Et vanlig mål for samsvar er «Intersection over union», forkortet IoU, som er definert som arealet som er markert både av fasiten og modellen (intersection), delt på arealet som er markert av modellen og fasiten til sammen (union). Ytelsesmålet vil da være gjennomsnittlig IoU-verdi over en samling test-eksempler. IoU fungerer best hvis objektet man skal segmentere er omtrent like stort for de forskjellige eksemplene.

For objektdeteksjon er oppgaven å markere områder hvor en bestemt type objekter finnes med et kvadrat eller en annen geometrisk form, uten å markere hver enkelt piksel som inngår i objektene. Ytelsen til et slikt system gjøres ved at man teller hvor mange objekter som fanges opp og hvor mange falske positive modellen markerer. Man kan også beregne IoU som for segmentering ved å sammenlikne med annoterte markeringer.

Generative modeller

Dagens KI-modeller kan produsere tekst, lyd og bilder. For generering av tekst kan dette for eksempel dreie seg om å lage automatiske sammendrag av pasienthistorikk basert på lagrede journalnotater, referater fra kliniske konsultasjoner, eller oversetting av brev til pasientens morsmål. For lyd kan det for eksempel bli aktuelt med automatisk tolketjeneste, som løpende oversetter norsk tale til pasientens språk. Man kan også tenke seg prateroboter (chatbots), som for eksempel tester befolkningen for kognitiv svikt eller gir samtaleterapi for pasienter med angst og depresjon. Bilde- og video-generering for medisinske formål ligger kanskje lenger fram, men man kan tenke seg modeller som automatisk produserer informasjonsmateriell, skreddersydd til en bestemt pasient.

Det er neppe mulig å definere generelle ytelsesmål som automatisk evaluerer generativ KI, men noen anvendelser av denne teknologien vil også falle inn under de kvantitative kategoriene over. Screening for kognitiv svikt med chatbot passer for eksempel inn i rammeverket for klassifisering eller regresjon, avhengig av om utdataene er diskrete eller kontinuerlige.

Eksempelet med chatbot som automatisert psykologtjeneste til behandling av angst og depresjon må vurderes på linje med medisinske intervensjoner generelt, fortrinnsvis med randomiserte kontrollerte studier. Selv om slike systemer kan være teknisk realiserbare i nær framtid, vil implementering i klinisk bruk sannsynligvis ligge et stykke fram i tid fordi validering av sikkerhet og effekt er utfordrende. Dersom KI-systemet er medisinsk utstyr så skal det samsvarsvurderes jf. MDR og CE-merkes.

Ytelsen til KI-systemer som genererer tekst til bruk for mer oppgaver må normalt testes gjennom vurderinger av brukergruppen. Hvis man for eksempel vil innføre en KI-modell for å lage sammendrag av sykehistorier til støtte for klinikere, må nødvendigvis de aktuelle klinikerne vurdere hvor nyttig den er.

En måte å måle ytelsen til en språkmodell på er å utarbeide testsett rettet mot spesifikke oppgaver og sammenligne svarene fra modellen med testsettet. Det kan for eksempel være predefinerte spørsmål og svar (ground truth).

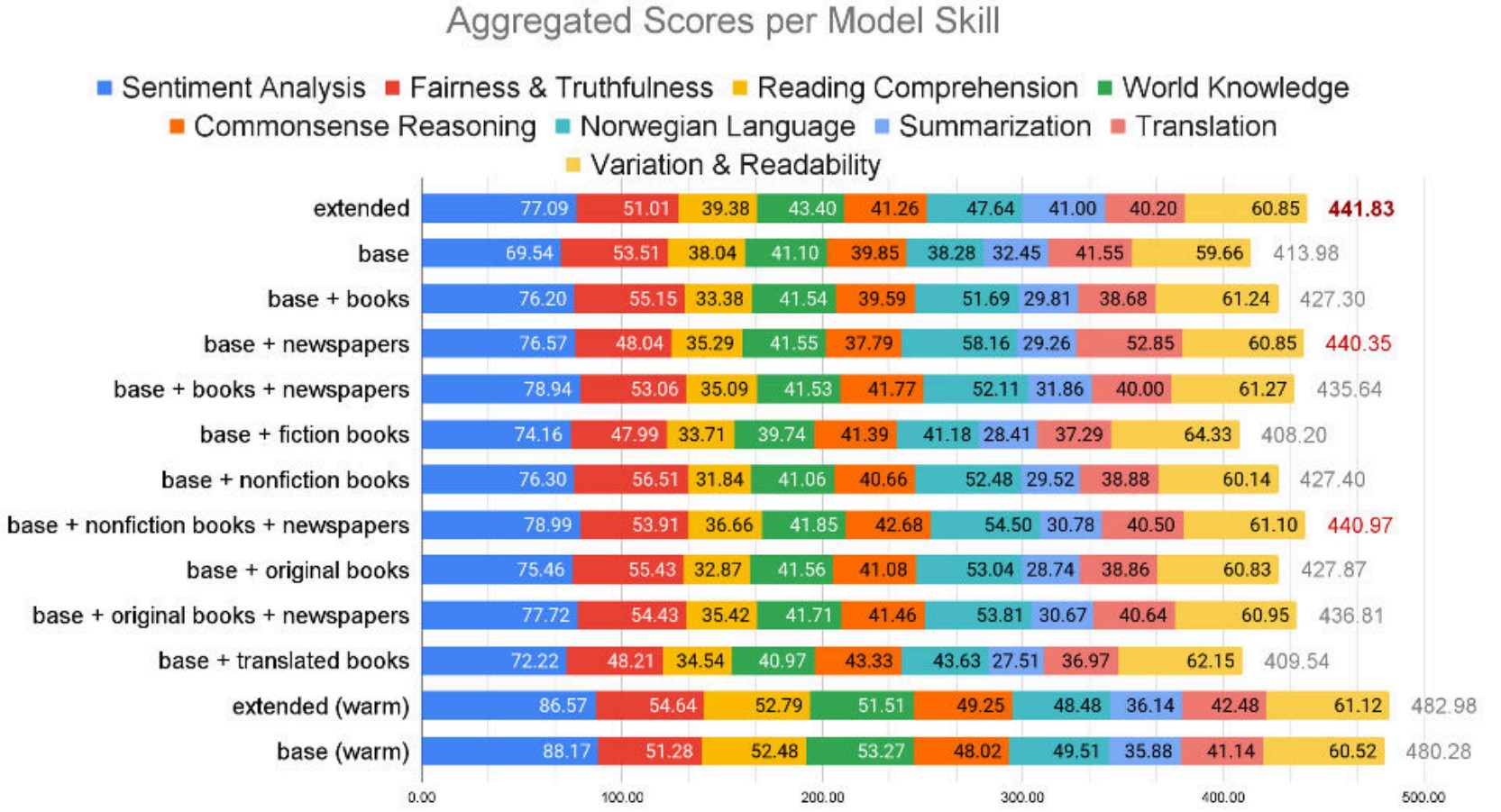
I Mímir-prosjektet har Nasjonalbiblioteket sammenlignet ytelsen til noen språkmodeller på tvers av en rekke språklige og naturlige oppgaver for språk, som tekstgenerering, oversettelse, spørsmål/svar og sentimentanalyse.⁵ Figuren under viser en sammenligning av hvordan ulike generative språkmodeller skårer på ulike ferdigheter som rettferdighet, sannferdighet og norsk språk.